Transfer Learning in Automatic Seismic Interpretation
Dramsch, J. S., & Lüthje, M. (2018). Deep-learning seismic facies on state-of-the-art convolutional neural network architectures. In SEG Technical Program Expanded Abstracts 2018 (pp. 2036-2040). Society of Exploration Geophysicists. |
|||
This chapter discusses transfer learning in asi. Transfer learning is a technique that uses a dnns pre-trained on a different data set that is usually larger and more diverse, which is then fine-tuned to the target data. dnns are notorious for needing large numbers of diverse annotated samples. That is often prohibitive to geoscience applications of machine learning, where data is expensive and difficult to acquire, labelling by experts is complicated and prone to bias (Bond et al. 2007), and often only available within commercial environments. In (Jesper Sören Dramsch and Lüthje 2018b) we show that sotas convolutional neural networks pre-trained on a natural image data set (ImageNet, cf. 2.2.2.4) can be transferred to perform asi. This paper forms the central contribution of this chapter.
In the computer vision community, hand-labelled data sets like ImageNet, CIFAR, and PASCAL-VOC are openly available, which catalyzed the development of new architectures and approaches in deep learning. Geoscientific data is often expensive to acquire, and companies are reluctant to make data available, even less so for processed or interpreted data. Early machine learning workshops often showed results on the open Dutch F3 dataset; however, national data repositories have started to change this approach to foster innovation. With data becoming more available recently, the next problem is the lack of ground truth. Obtaining accurate labels for seismic data is impossible, as any inversion process is non-unique and digging is not practical. In other imaging-based fields (e.g. radiology) that rely on the interpretation of imaging results, studies investigate both inter-interpreter variations, by making several interpretations available and intra-interpreter variability by re-interpreting the dataset after a set time interval (McErlean et al. 2013; Alikhassi, Gourabi, and Baikpour 2018; Al-Khawari et al. 2010). Additionally, simulations provide ground truth, but can implicitly include modelling assumptions in the data or commit the inverse crime (Wirgin 2004). The inverse crime presents the problem of modelling and inverting data with the same theoretical ingredients.
In geophysics itself, seismic data presents a unique challenge to computer vision problems. Displays of seismic data usually clip amplitudes in the 3rd to 5th percentile to make most of the seismic amplitude content visible. These particularly strong amplitudes make up a very small number of the distribution of amplitudes. However, they have to be contained within the constant dynamic range of the data, while adding minimal information gain (Forel, Benz, and Pennington 2005). Moreover, limiting these outlier amplitudes decompresses the main distribution of amplitudes over the full dynamic range. This becomes particularly important when compressing data to lower bitrates, i.e. from 32-bit floats to 16-bit floats. Clipping amplitudes has also proven to be a viable preprocessing step before feeding seismic data to computer vision systems, such as convolutional neural networks. Machine learning systems have been known to be vulnerable to noise. This noise can be physical noise (e.g. low snr) for simpler models or adversarial attacks that reverse engineer more complex models. These adversarial attacks on machine learning models attempt to find vulnerabilities in the trained models intentionally. Frequently, these adversarial attacks can provide insights into edge-behaviours and susceptibility to noise. Adversarial attacks include a one-pixel attack on ImageNet classifiers, which changes a single value in an image to cause a misclassification (Su, Vargas, and Sakurai 2019). Humanly imperceptible noise changes the digital image so slightly that the human eye cannot see a change, but the classifier is led to misclassify the image (I. J. Goodfellow, Shlens, and Szegedy 2014), which is particularly interesting to physical applications of machine learning, that can have significant amounts of noise in their data. Alternatively, even physical printed stickers are used to fool a convolutional neural network in real-world applications (Brown et al. 2017). Besides, geological data contains regions of geological interest and regions that are inconsequential to geological interpretation. This selective interpretation of geological features, which has been common in seismic interpretation, as well as, well-log interpretation is challenging to represent in metrics adequately (S. Purves, Alaei, and Lolis 2019).
Realistically, the limited availability of labelled ground truth data can be addressed in different ways. In the case when labels are available but not abundant, transfer learning of highly generalizable models like VGG-16 can be fine-tuned to seismic data. The VGG-16 architecture can also be included in U-Nets as a decoder to leverage the benefits of transfer learning in semantic segmentation tasks (Jesper Sören Dramsch and Lüthje 2018b). Moreover, weakly-supervised training can perform label propagation of labelled subsections of the full data set to unlabeled sets. Unsupervised or self-supervised training can be applicable, where no reliable ground truth is available. Unsupervised training is applicable, when a desired operation on the data is known, or an internal structure of the data can be exploited (Jesper Sören Dramsch, Christensen, et al. 2019). Additionally, multi-task learning has been shown to be able to stabilize network performance in nlp (X. Liu et al. 2019) and rl (Yu et al. 2019).
Research into deep convolutional networks showed that the data in the network would lose signal with increasing depth, named vanishing gradient problem (Hochreiter 1998). This vanishing gradient problem led to the limitation of VGG at 19 layers; this is detailed further in 2.2.2.6. Residual blocks introduced a solution to this problem by implementing a shortcut between the original data and the output from the block. Chapter 2.14 presents the original ResNet block architecture, which was used in ResNet-50 and ResNet-101 in Figure 4.1 (K. He et al. 2016). Details on ResNet blocks differ, the main take-away being the sum or concatenation of the original data with the block output. DenseNets (G. Huang et al. 2017) and Inception-style networks (Szegedy et al. 2015) are other approaches to build deeper neural networks.
![Top-5 Accuracies of Neural Architectures on ImageNet plotted against Million Parameters, color-coded to similar network type. Data and references shown in `[tab:imagenet-sota] <#tab:imagenet-sota>`__](../images/imagenetsota.png)
Top-5 Accuracies of Neural Architectures on ImageNet plotted against Million Parameters, color-coded to similar network type. Data and references shown in [tab:imagenet-sota]
Figure 4.1 additionally contains several classes of neural network architectures, namely AmoebaNet, NASNet, and EfficientNet. These categories are a more recent development in neural architecture research, based on nas, which automates the search for novel architectures instead of completely hand-tuning new developments. This optimization scheme to search for neural architectures has been developed to include different optimization objectives. The AmoebaNet is based on ec, a numeric optimization technique mimicking biological evolution, and subsequent fine-tuning of the solution to search for an ideal neural architecture to perform image classification (Real et al. 2019). The NASNet goes on with fixed overall architecture, but uses a controller rnn to modify the blocks within the architecture (Zoph et al. 2018). The EfficientNet architecture was also acquired by nas, by optimizing for both accuracy and flops. Optimizing for flops reduces the computational cost of the final architecture (Tan and Le 2019a). Moreover, Tan and Le (2019a) derives a method of simultaneously scaling multiple dimensions in deep neural networks named compound scaling. The standard ResNet-50 and ResNet-101 differ only in-depth, whereas compound scaling establishes a relationship between depth, width and resolution-scaling of deep neural networks using a single scaling parameter.
VGG-16 and ResNet-52 are two network architectures that are used in the paper in this chapter. These can be identified in Figure 4.1. The performance of both models in the Top-5 accuracy on ImageNet is comparable, while the number of parameters vastly differ. VGG-16 contains 138 million parameters, while ResNet- 52 contains 23 million parameters, the VGG-16 network is, however, 16 layers deep, while Resnet-52 contains 52 layers. These networks are compared to the end-to-end trained convolutional neural network built by Anders Waldeland and Solberg (2016).
Training and Fine-Tuning
The training of the three networks in this chapter, namely Waldeland CNN, VGG-16, and Resnet-52, requires different strategies to obtain optimal results. The Waldeland convolutional neural network is end-to-end trained on the training data. The VGG-16 and ResNet-52 are fine-tuned with pre-trained weights, which require a lower learning rate and fixing the weights in parts of the network. The networks are trained with the categorical cross-entropy loss discussed in equation [crossentropy]. The categorical cross-entropy enables training on multi-class labels by optimizing the multi-variate negative log-likelihood. It is reprinted here for convenience:
The VGG-16 model has the first seven layers frozen. The ResNet-52 has the first 44 layers frozen. This ensures that the most general features are preserved, while higher abstraction features in layers can be adjusted to the training data. Moreover, the last layer that outputs the classification has to be replaced by an appropriate layer, which instead of predicting 1000 classes for ImageNet, predicts the number of classes in our training set 9.
The training relies on the custom loader presented in [code:loader]. This loader extracts patches from the 2D seismic image and the according label and provides a convenient generator. This generator can perform the data preparation on CPU while the training is performed on GPU. Additionally, the training is monitored to implement an early-stopping procedure. This enables us to stop the training when the validation loss and validation accuracy deteriorate. This avoids overfitting of the network, which is particularly essential when fine-tuning an over-parametrized network to smaller-scale data.
End-to-End convolutional neural network training
The training of the Waldeland convolutional neural network is trained end-to-end. The optimizer for the Waldeland convolutional neural network is the Adam optimizer (Diederik P. Kingma and Ba 2014) with a learning rate of \(0.001\), the decay of first-order moments of \(\beta_1=0.9\), and second-order moments of \(\beta_2=0.999\).
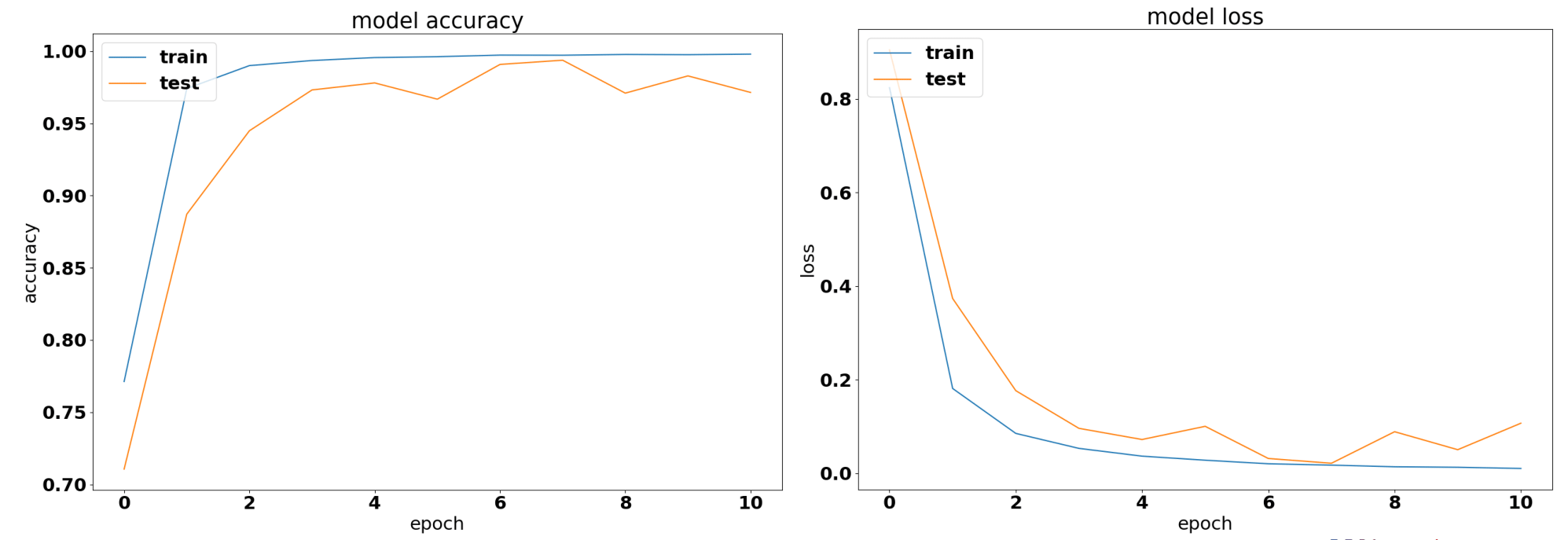
Accuracy and Categorical Cross Entropy for Waldeland convolutional neural network
Figure 4.2 shows the training loss of end-to-end training. The accuracy shows that the network very quickly reaches 100% accuracy on the training data while performing close to perfect on the test set. The training is stopped after ten epochs. The loss shows that the model starts overfitting at epoch 7. A dataset with more diverse labels and samples would improve this situation.
Fine-Tuning Pre-Trained Networks
Pre-trained networks were trained on a dataset and made available by the researchers and companies, including weights and biases. These are often trained on large corpuses of data. In computer vision, classically pre-trained networks were trained on ImageNet, CIFAR, and PASCAL-VOC. The sota networks are pre-trained on up to a billion images with 17,000 labels and subsequently fine-tuned on the ImageNet-1K dataset (Mahajan et al. 2018). This strategy is applied across deep learning, including computational linguistics with 175 billion parameters pre-trained on 0.499 trillion words in GPT-3 (Brown et al. 2020). The pre-trained networks in this chapter were trained on the ImageNet corpus and transferred to the MaleNov seismic dataset (Ildstad and Bormann 2017).
The VGG-16 and ResNet-52 are finetuned using sgd with Nesterov momentum. The learning rate for the sgd is set to \(0.0001\), with a momentum of \(0.9\). Additionally, a learning rate schedule is implemented that updates the learning rate (lr) according to \(lr(t) = 0.0001 \cdot \left( 1 + 10^{-6} \cdot t \right)^{-1}\).
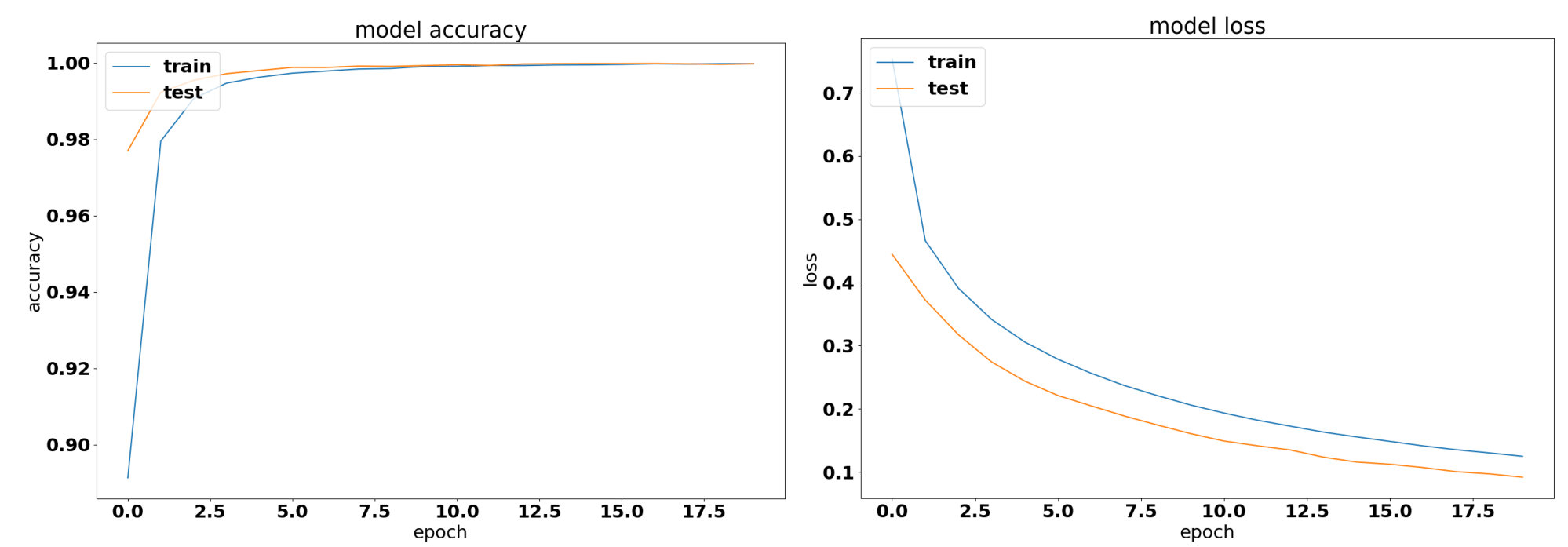
Accuracy and Categorical Cross Entropy for VGG16 convolutional neural network
The VGG-16 network quickly converges to 100% accuracy, the loss, however smoothly converges towards a cross-entropy of \(0.1\). The network does not show signs of overfitting and trains the full 20 epochs. With the available hardware at the time of writing the paper and the good results despite possibly increasing the convergence.
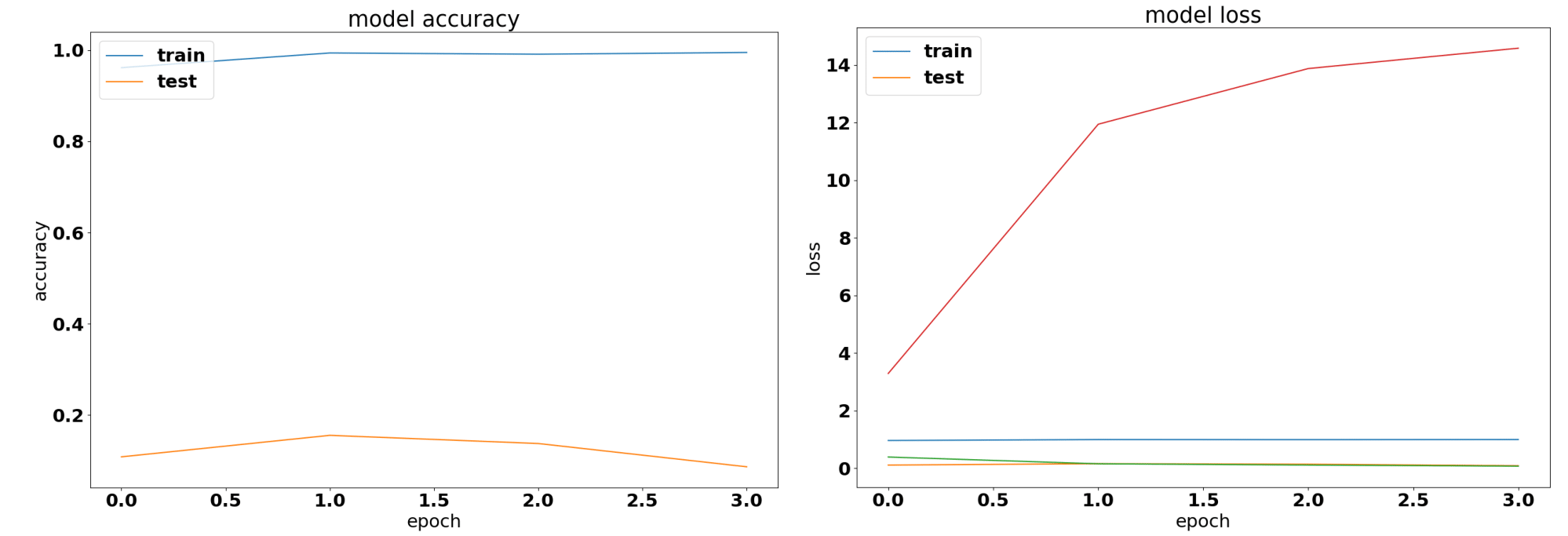
Accuracy and Categorical Cross Entropy for ResNet52 convolutional neural network
The ResNet-52 network immediately reports a training accuracy of close to 100% while the test data report 11% accuracy, which is a performance equivalent to random chance on this dataset containing nine classes. The loss in Figure 4.4 shows the same problem of a massively overfit network. For this reason, the network predictions were not displayed in the paper in this chapter.
Conference Paper: Deep learning seismic facies on state of the art convolutional neural network architectures
Introduction
Seismic interpretation is often dependent on the interpreters experience and knowledge. While deep learning cannot replace expert knowledge, we explore the accuracy of convolutional networks in interpreting seismic data to support human interpretation.
In the 1950s neural networks started as a simple direct connection of several nodes in an input layer to several nodes in an output layer (Widrow and Lehr 1990). In geophysics this puts us to the introduction of seismic trace stacking (Öz Yilmaz 2001). In 1989 the first idea of a convolutional neural network was born (Lecun 1989) and back-propagation was formalized as an error-propagation mechanism (D. E. Rumelhart, Hinton, and Williams 1988). In 2012 the paper (Krizhevsky, Sutskever, and Hinton 2012a) propelled the field of deep learning forward implementing essential components, namely GPU training, ReLu activation functions (Dahl, Sainath, and Hinton 2013) and dropout (Srivastava et al. 2014). They outperformed previous models in the ImageNet challenge (J. Deng et al. 2009) by almost halving the prediction error. Anders Waldeland and Solberg (2016) showed that neural networks can be used to classify salt diapirs in 3D seismic data. Rutherford Ildstad and Bormann (2017) generalized this work to nD and beyond two classes of salt and "else".
The task of automatic seismic interpretation can be equated to dense object detection (T.-Y. Lin et al. 2017) or semantic segmentation. These tasks are currently best solved by Mask R-CNN architectures (Long, Shelhamer, and Darrell 2015). Statoil has used U-Nets for automatic seismic interpretation. Yet, classification networks can be used for semantic segmentation, but are significantly slower. The benefit is a testable example of generalization of pre-trained networks form photographic data to seismic images. As well as, a testable framework for choosing hyper-parameters for neural networks on seismic data.
Deep learning relies heavily on vast amounts of labeled data to train on initially. However, the features learned from these networks can often be transferred to adjacent problem spaces (Baxter 1998). Often these transfer learning tasks are tested on photographs rather than seismic or medical imaging tasks. The aim of this study is to evaluate state-of-the-art pre-trained networks in the task of automatic seismic interpretation. We compare three convolutional neural networks of increasing complexity in the task of supervised automatic seismic interpretation. We evaluate these tasks qualitatively and quantitatively.
Methods
The neural networks in this study learn supervised. The features were published alongside the open source framework MalenoV and describe nine seismic facies in the open F3 data set. The classes describe steep dipping reflectors, salt intrusions, low coherency regions, low amplitude dipping reflectors, high amplitude regions continuous high amplitude regions and grizzly amplitude patterns presented in Figure 4.7. Additionally, a catch-all “else” region are picked. In this approach we chose Keras (Chollet and others 2015a) with a Tensorflow (Abadi et al. 2015a) backend on a K5200 GPU at DHRTC. Keras is a high level abstraction of tensor arithmetics. Tensorflow is an open source numerical computation library on static graphs. We train 2D convolutional neural networks (CNN) of varying depth on seismic slices to propagate single slice interpretations to a volume. CNNs are highly flexible models for computer vision tasks.
Network one depicted in Figure 4.5 was developed by (Anders Waldeland and Solberg 2016) to identify salt bodies in 3D seismic data. Three layers are fully connected for classification. The network uses a kernel of 5 by 5 pixels for convolution and a stride of 2 for down-sampling. We use the Adam optimizer and cross-categorical entropy as a loss function. The Adam optimizer is an extension to stochastic gradient descent (SGD) that implements adaptive learning rates and bias correction (Ruder 2016). We add dropout and batch normalization to the network. These methods improve regularization and prevent overfitting. Furthermore, we use early-stopping to prevent overfitting the model by over-training. We chose two metrics to monitor in the training and validation sets, namely mean absolute error and accuracy. The Waldeland convolutional neural network is relatively shallow compared to modern deep learning networks with 95,735 parameters to optimize for.
Waldeland convolutional neural network architecture. Input at the Top. Softmax Classification
Layer on bottom. Width of objects shows log of spatial extent of
layer. Height shows log of complexity of layer. The layers are
color coded to show similar purpose.
Network two is the VGG16 network (Simonyan and Zisserman 2014b) by the Visual Geometry Group. It contains 16 layers and 1,524,2605 parameters. 13 of these layers ore convolutional layers with a 3x3 kernel. Convolutional blocks are interspersed with max-pooling layers for down-sampling. The last three layers are fully connected layers for classification. The VGG16 architecture was proposed for the ImageNet challenge in 204. It is widely used for it’s simplicity in teaching and it’s generalizability in transfer learning tasks.
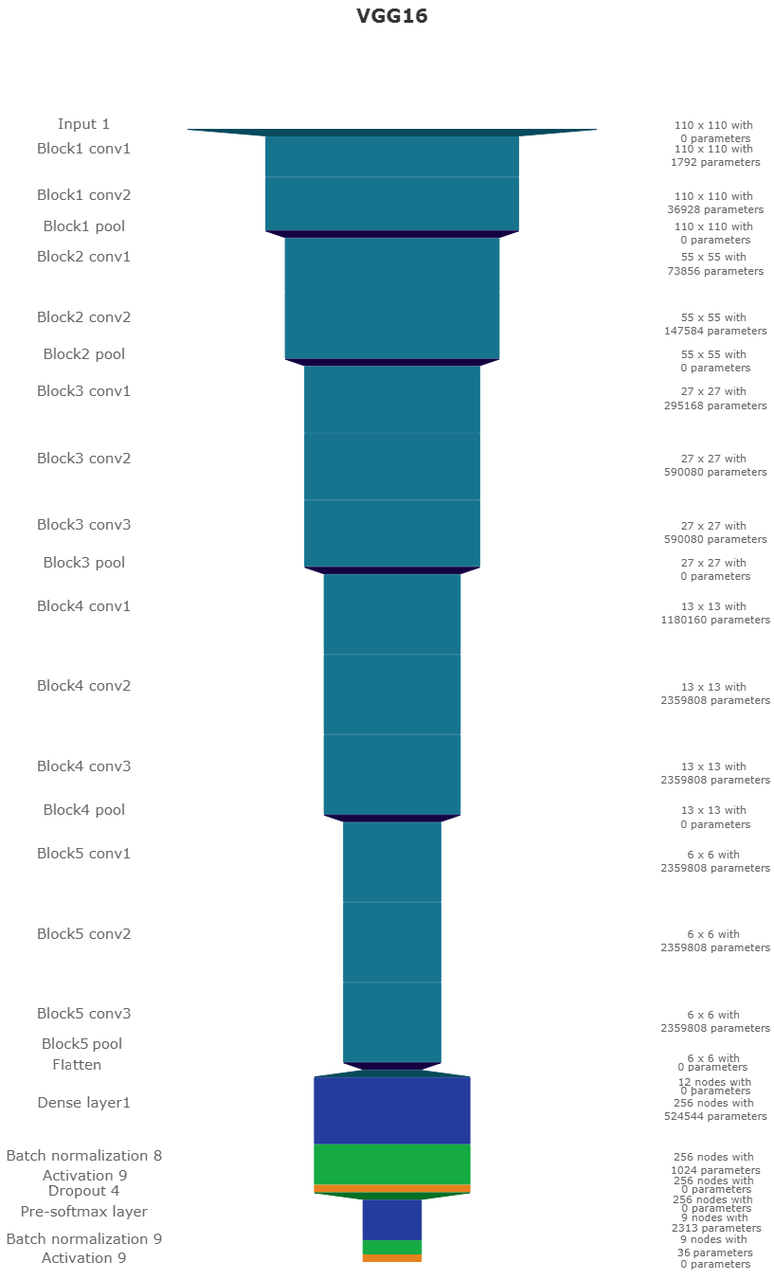
VGG16 architecture. Same visualization as Figure 4.5
Network three is the ResNet50 architecture by Microsoft. The network consists of 50 layers with 2,361,6569 parameters. It implements a recent development, called residual blocks. These residual blocks add a skip- or identity-connection around a stack of 1x1, 3x3, 1x1 convolutional layers (K. He et al. 2016). The 1x1 are identity convolutions, used for down- and subsequent up-sampling to decrease the computational cost of very deep convolutional neural networks. The convolutional layers are followed by one fully connected layer for classification.
All networks use rectified linear units (ReLu) as neural activation. The last layer uses Softmax as activation to output a probability for each class. Training both VGG16 and the ResNet50 end to end would be very expensive. These models have been trained on big labeled data that are not available in geoscience. However, transfer learning enables us to use pre-trained networks on very different tasks. In transfer learning, we use the learned weights of the networks and replace the fully connected layers. These untrained layers are specific to our task and have to be fine-tuned to the data. This process is very fast and requires little data. We fine-tune an entire network on one sparsely interpreted 2D seismic slice. For the fine-tuning process, we replace the Adam optimizer by a classic SGD optimizer with lower learning rate, very low weight decay and Nesterov momentum. We still use early-stopping on validation loss and cross-categorical entropy.
We added the same fully connected layer architecture to VGG16 and ResNet50 that Waldeland added to their architecture. Therefore, we test if pre-trained convolution kernels are fit to recognize texture features in seismic data. We set up a validation set to quantify the accuracy of our networks on previously unseen data. Additionally, we set up a prediction pipeline to populate each one 2D inline and crossline of the seismic data to qualitatively visualize the prediction capability of the networks. The labels for the supervised interpretation are taken from the MalenoV interpretation by ConocoPhillips, shown in Figure 4.7.
Network |
Run |
Loss |
MAE |
Acc |
|---|---|---|---|---|
Waldeland CNN |
Training |
0.001 |
0.000 |
100.0% |
Test |
0.003 |
0.000 |
99.9% |
|
VGG16 |
Training |
0.010 |
0.005 |
99.8% |
Test |
0.127 |
0.026 |
100.0% |
|
ResNet50 |
Training |
0.011 |
0.001 |
100.0% |
Test |
14.166 |
0.195 |
12.1% |
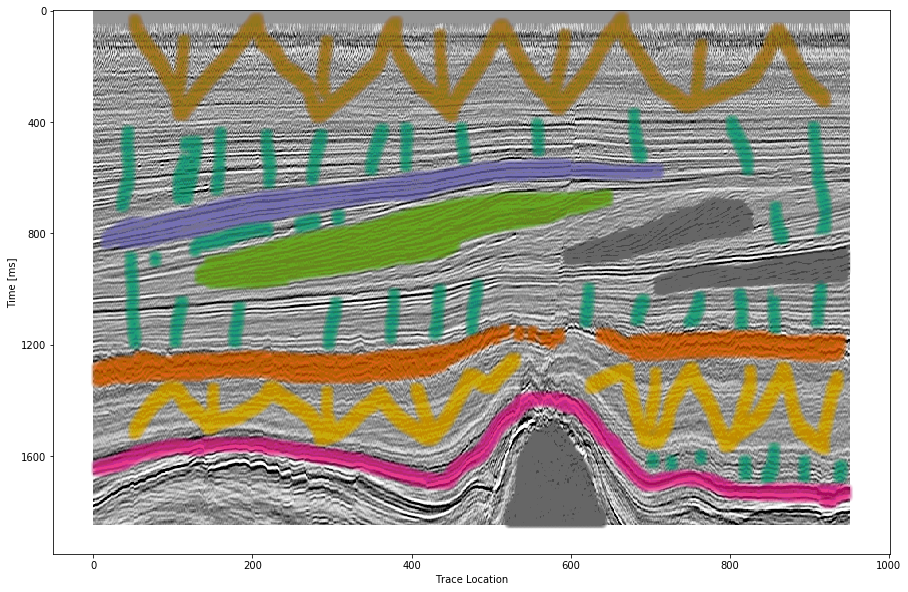
Labeled data set on one 2D inline slice. Color interpretation: Low coherency (brown), Steep dipping reflectors (gray), low amplitude dipping reflectors (grass green), continuous high amplitude regions (blue), grizzly (orange), low amplitude (yellow), high amplitude (magenta), salt intrusions (gray), else (turquoise).
Results
We use the open Dutch F3 data set to calibrate our predictions. Crossline 339 has been interpreted by ConocoPhillips and made available freely. We show results of crossline slice 500. We have used the same plotting parameters for both either results, both have been generated programatically, without human intervention. Figure 4.8 (a) shows the prediction of the Waldeland convolutional neural network at every location of the 2D slice based on a 65 x 65 patch of the data. Border patches were zero padded. We see clear patches for the low coherency region in brown. The low amplitude dipping (grass green) region has been reproduced well, however some regions at \(t\approx1080~\text{ms}\) have been marked incorrectly, where two seismic packages meet. This faulty region also contains patches that were interpreted as low amplitude region (yellow). While this may be a low amplitude region, we expect the packages to be largely continuous, which leaves this interpretation as questionable at best. The gray area was reproduced well, however it was marked as salt body in the original manuscript, this would be incorrect here. We see the grizzly amplitude pattern (orange) and the low amplitude (yellow) regions are well-defined and separated. The underlying package of high amplitudes has been identified will. However, between location 600 - 800 the top part was marked as "else" (turquoise), which undesirable but correct, judging from the texture. Here, retraining would be possible by feeding this relabeled region to the network. Below this region, the networks predictions become erratic. The classification is blocky between grizzly and salt with "else" interspersed. However, the edges will often give problems due to the padding. Around location 800 high amplitudes (orange) have been mislabeled as grizzly amplitudes.
The VGG16 network classification is shown in Figure 4.8 (b). The network performs similar to the Waldeland convolutional neural network in Figure 4.8 (a), however some key differences will be pointed out. The separation of low coherency and the "else" region around \(t\approx400~\text{ms}\) is less defined and, therefore, worse. The coherency of low amplitude dipping (grass green) and high amplitude continuous (blue) is worse in the region around location 280, \(t\approx800~\text{ms}\). This might be due to higher sensitivity to declines in seismic quality. Below \(t\approx1000~\text{ms}\) the "else" region is free from differing patches, in contrast, the Waldeland convolutional neural network interspersed two other classes in this region. VGG16 also classifies some "else" regions in the high amplitude (magenta) region between location 600-800. The area around location 200 below the high amplitude (magenta) region is also blocky, although less so. The misclassification of the bottom high amplitude (magenta) region as grizzly (orange) is less pronounced in the VGG16 interpretation. It is present toward the bottom left corner.
The results of the ResNet50 are not shown. The network classifies all seismic facies as "else". This indicates that the network is overfitting the data. This is supported by the numeric results presented in table Figure 4.1. The network training error indicates a perfect fit to the data, whereas the test score is unseen data with labels to evaluate the performance of networks on unseen data. While both the Waldeland convolutional neural network and VGG16 perform well, the ResNet50 performs very poorly.
|
|
Figure 4.8: Automatic seismic interpretation with CNNs. Color interpretation: Low coherency (brown), Steep dipping reflectors (gray), low amplitude dipping reflectors (grass green), continuous high amplitude regions (blue), grizzly (orange), low amplitude (yellow), high amplitude (magenta), salt intrusions (gray), else (turquoise).
Conclusion
Convolutional neural networks show good results for propagating interpretations through seismic cubes. The pre-trained VGG16 convolutional neural network has shown very good results in adapting to seismic texture identification. Transfer learning was fast and the results are similar to the shallower Waldeland convolutional neural network. Both networks have trade-offs in the misclassification and can be improved upon.
The ResNet50 was shown to be ineffective on transfer learning seismic data with pre-trained weights. This is in accordance with results from other attempts at transfer learning. The ResNet filters are more specific to photography and transfer poorly to other data sources, where the VGG learned features prove to be more general to computer vision tasks. More complicated architectures may perform well, trained directly with the according data, but they learn specific features fit for the problem space that do not transfer well.
Acknowledgments
The authors would like to thank the DHRTC and DUC for their continued support. We thank Colin MacBeth, Peter Bormann, Sebastian Tølbøll Glavind, Lukas Mosser and the "Software Underground" community for great discussion and support with MalenoV and ConocoPhillips for making the data and software freely available. We also thank Agile Scientific for great tutorials at the intersection of Python and geoscience. We thank dgb for providing the F3 data set.
Applications of Transfer Learning for Automatic Seismic Interpretation
Figure 4.8 (a) shows the results of a fully trained network compared to a pre-trained network. The pre-trained network decreases both training time and data requirements significantly, while not compromising accuracy. A pre-trained network with diverse generalizable learned filters seems to alleviate some limitations of smaller non-diverse data sets used in the fine-tuning process. These pre-trained networks themselves are of little use to most applications in geoscience. Nevertheless, they can be integrated into more task-appropriate neural network architectures that leverage the pre-training.
Apart from building deeper networks for image classification, the neural architectures can serve as a forcing function to the task the network is built for. Encoder-Decoder networks will compress the data with a combination of downsampling layers, which in the case of a computer vision could either be strided convolutions or pooling layers after convolutional layers. During these operations, the number of filters increases, while the spatial extent is diminished significantly. This encoding operation is equivalent to lossy compression, with the low-dimensional layer called "code" or "bottleneck". The bottleneck is then upsampled by either strided transpose Convolutions or upsampling layers that perform a specified interpolation. This is the decoder of the Encoder-Decoder pair. These networks can be used for data compression in aes, where the decoder restores the original data as good as possible (Hinton and Salakhutdinov 2006). Alternatively, the decoder can learn a dense classification task like semantic segmentation or seismic interpretation.
U-Nets present a special type of encoder-decoder networks that learn semantic segmentation on from small datasets (Ronneberger, Fischer, and Brox 2015a). They form a special kind of fcn shown in Chapter 2.15. Originally developed on biomedical images, the network found wide acceptance in label-sparse disciplines. The U-Net implements shortcut connections between convolutional layers of equal extent in the Encoder and Decoder networks. This alleviates the pressure of the network learning and reconstructing the output data from the bottleneck in isolation.
The data set in this training is very small and non-diverse as shown in Figure 4.7 and this only made training on a classification network possible. Image segmentation would need a dense labelling of the training data and more than one 2D section available. This has been approached by Alaudah et al. (2019) by labelling the full Dutch F3 dataset, which cites the paper presented here. Modern applications of transfer learning were able to leverage ResNet architectures as an encoder in U-nets on seismic data (Babakhin, Sanakoyeu, and Kitamura 2019a).
Contributions of this Study
This study introduced transfer learning for deep learning tasks in asi and has found an application across geophysics (see e.g. Babakhin, Sanakoyeu, and Kitamura 2019b; G. Li et al. 2019; M. Liu et al. 2019). The transfer learning enables utilizing neural networks that were trained on a diverse dataset and then fine-tuning them with data that contains far fewer samples. This outperforms smaller networks that can be trained end-to-end on these small datasets. The code is available at https://github.com/JesperDramsch/seismic-transfer-learning.